Lista De Exercícios Sobre Equação Do 2º Grau – Brasil Escola: mergulhe nesse universo de desafios matemáticos! Equações do segundo grau são fundamentais em diversas áreas, da física à engenharia financeira. Dominar seus métodos de resolução – Bhaskara, fatoração, soma e produto – é crucial para resolver problemas complexos e interpretar resultados com precisão. Prepare-se para aprimorar suas habilidades e enfrentar exercícios que irão testar seus conhecimentos e expandir sua compreensão dessa ferramenta matemática poderosa.
Este material abrange diferentes tipos de equações (completas e incompletas), detalha os métodos de resolução, compara sua eficiência e apresenta aplicações práticas em áreas como física (lançamento de projéteis), geometria (cálculo de áreas) e finanças. A interpretação do discriminante (delta) e a análise crítica das soluções também são abordadas, garantindo uma compreensão completa do assunto.
Aplicações Práticas de Equações do 2º Grau

As equações do 2º grau, apesar de parecerem um tópico abstrato da matemática, possuem aplicações práticas em diversas áreas do conhecimento, sendo ferramentas essenciais para resolver problemas em física, geometria e finanças, entre outras. Sua utilização permite modelar situações reais e encontrar soluções para problemas que, à primeira vista, parecem complexos. Neste texto, exploraremos alguns exemplos concretos de como essas equações são utilizadas no dia a dia.
Lançamento de Projéteis
A trajetória de um projétil, como uma bola lançada ao ar, pode ser descrita por uma equação do 2º grau. Considerando a resistência do ar desprezível, a altura (h) em função do tempo (t) é dada pela equação:
h(t) = -gt²/2 + v₀t + h₀
onde g é a aceleração da gravidade (aproximadamente 9,8 m/s²), v₀ é a velocidade inicial vertical e h₀ é a altura inicial.Vamos considerar um exemplo: Uma bola é lançada verticalmente para cima com velocidade inicial de 20 m/s a partir do solo (h₀ = 0). Para descobrir em que instante a bola atingirá a altura de 15 metros, podemos substituir os valores na equação: 15 = -9,8t²/2 + 20t +
- Simplificando, obtemos a equação do 2º grau: 4,9t²
- 20t + 15 = 0. Resolvendo esta equação utilizando a fórmula de Bhaskara, encontramos dois valores para t, representando os instantes em que a bola passa pela altura de 15 metros (uma vez na subida e outra na descida).
Problemas de Geometria, Lista De Exercícios Sobre Equação Do 2º Grau – Brasil Escola

Equações do 2º grau são frequentemente utilizadas na resolução de problemas geométricos, principalmente aqueles envolvendo áreas e perímetros. Um exemplo clássico é o cálculo das dimensões de um retângulo, conhecendo sua área e o perímetro ou uma relação entre suas dimensões.Imagine um retângulo cuja área é de 36 m² e cujo perímetro é de 26 m. Sejam x e y as dimensões do retângulo.
Temos duas equações: xy = 36 (área) e 2x + 2y = 26 (perímetro). Da segunda equação, podemos isolar y: y = 13 – x. Substituindo na primeira equação, obtemos x(13 – x) = 36, que resulta na equação do 2º grau: x²13x + 36 = 0. Resolvendo essa equação, encontramos as dimensões do retângulo.
Problemas Financeiros

Em finanças, equações do 2º grau podem ser aplicadas em cálculos de juros compostos, determinação de pontos de equilíbrio em modelos de custos e receitas, entre outras aplicações. Por exemplo, em um investimento com juros compostos, a equação do 2º grau pode ser usada para determinar o tempo necessário para um investimento atingir um determinado valor.
Interpretação e Análise de Resultados: Lista De Exercícios Sobre Equação Do 2º Grau – Brasil Escola

A resolução de uma equação do segundo grau, utilizando a fórmula de Bhaskara, não se limita à obtenção das raízes. A interpretação do resultado, incluindo a análise do discriminante (delta), é crucial para a compreensão completa do problema e a validação da solução no contexto apresentado. Este processo garante a coerência e o significado prático da resposta matemática obtida.O discriminante (Δ = b²4ac) da fórmula de Bhaskara indica a existência e a natureza das raízes da equação.
Sua análise permite classificar as soluções como reais e iguais, reais e diferentes, ou complexas (não reais). Essa classificação tem implicações diretas na interpretação do problema em questão, especialmente em contextos aplicados, onde as raízes representam grandezas físicas ou valores reais.
O Discriminante e a Natureza das Raízes
O valor do discriminante determina a natureza das raízes da equação do segundo grau. Se Δ > 0, a equação possui duas raízes reais e distintas. Se Δ = 0, a equação possui duas raízes reais e iguais (uma raiz real dupla). Se Δ < 0, a equação não possui raízes reais; suas raízes são complexas (envolvem o número imaginário i). É importante notar que, em muitos problemas práticos, raízes complexas indicam que o problema, tal como formulado, não possui solução real.
Validação da Solução no Contexto do Problema
A mera obtenção das raízes de uma equação do segundo grau não garante que estas sejam soluções válidas para o problema em questão.
A análise do contexto é fundamental para validar os resultados. Por exemplo, em problemas que envolvem medidas físicas (comprimento, tempo, etc.), as raízes devem ser números reais e positivos. Raízes negativas ou complexas, nesses casos, não têm significado físico e devem ser descartadas.
Exemplos de Problemas com Raízes Não Viáveis
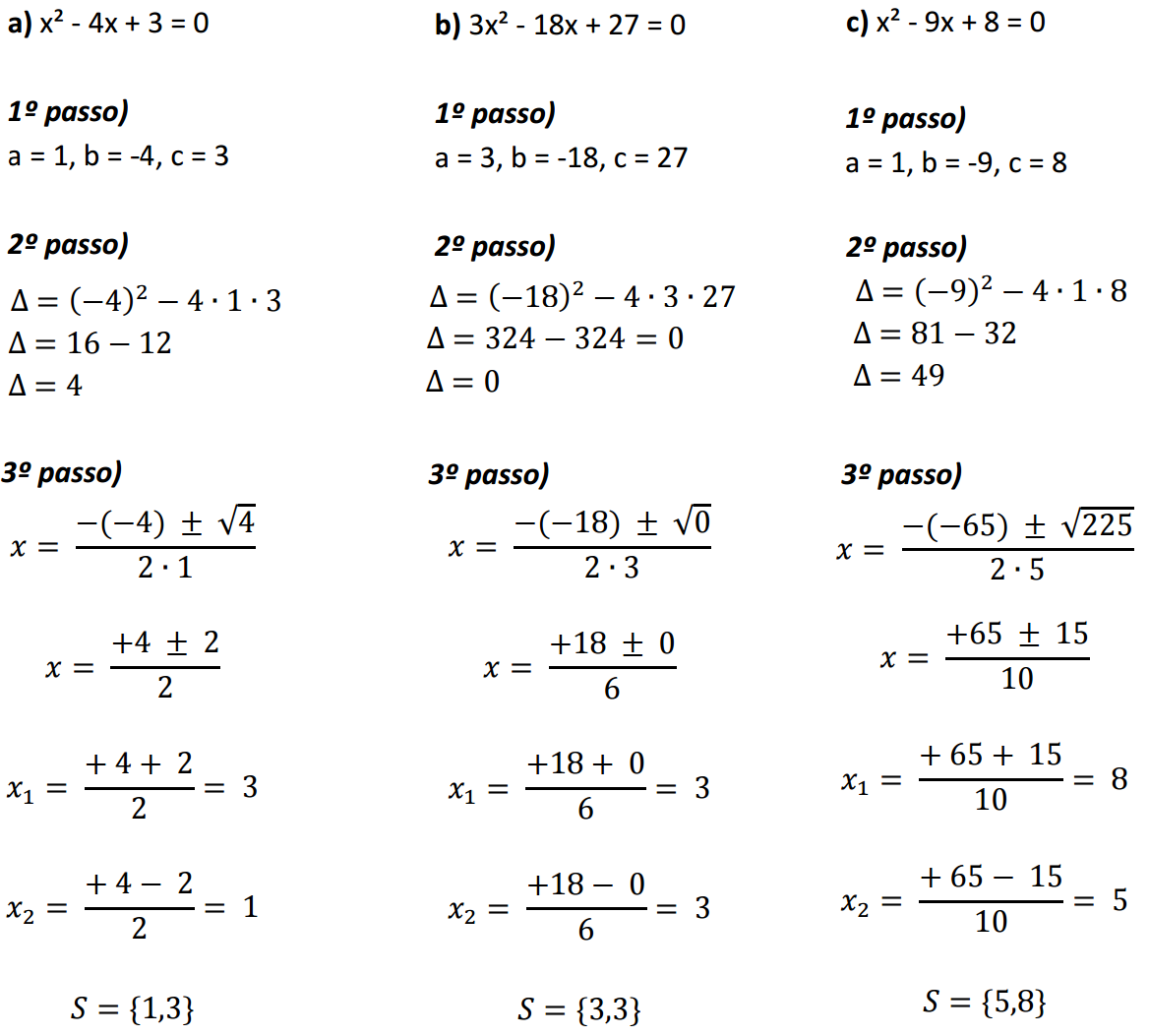
Considere um problema que busca calcular as dimensões de um retângulo, cuja área é 100 m² e o perímetro é 40 m. A formulação matemática pode levar a uma equação do segundo grau. Se as raízes encontradas forem, por exemplo, 10 e -5, a raiz negativa (-5) não tem significado físico, pois um comprimento não pode ser negativo. Portanto, apenas a raiz 10 é uma solução válida para o problema.
Outro exemplo seria um problema de cinemática que resulta em uma raiz negativa para o tempo. Tempo negativo não existe no contexto físico, tornando essa raiz inválida. Similarmente, um problema que calcula a altura de um objeto lançado para cima, onde a equação resultante apresenta raízes complexas, indica que o objeto não atingirá a altura especificada nas condições do problema.
Neste caso, a equação não representa a realidade do problema proposto.
Ao concluir esta lista de exercícios, você terá consolidado seu conhecimento sobre equações do segundo grau, desenvolvendo a capacidade de resolver problemas diversos e interpretar os resultados obtidos. A prática constante é a chave para o domínio dessa ferramenta matemática essencial. Lembre-se: a matemática não se limita a fórmulas; ela é uma poderosa ferramenta para modelar e solucionar problemas do mundo real.
Continue praticando e explore ainda mais os desafios que a matemática oferece!

